기초 논리학과 증명
이 단원에서는 기초적인 논리학과 증명에 대해 배운다. 수학을 공부함에 있어서 어떻게 정확히 타당한 수학적 논증(증명)을 만들어 내는지 이해하고 있어야한다. 이를 위해서는 논증에 사용되는 논리 규칙들과 명제들에 대한 공부가 먼저 선행되어야 한다. 논리 규칙들은 수학적 문장들의 의미를 좀 더 명료하게 하고, 이들에 대한 이해를 높여준다.
이 단원에서는 이를 위해 기초적인 명제/술어 논리학과 증명에 관해 다룰 것이다.
명제와 술어 논리(Proposition and Predicate Logic)
명제(Proposition)
명제 (proposition)는 참/거짓을 판정 할 수 있는 문장을 의미한다. 즉, 명제인 문장은 참이나 거짓 둘중 하나의 값을 가지게 된다. 이때, 둘 모두일 수는 없는데, 이러한 경우 판정할 수 없는 문장으로 명제가 아니게된다. 명제를 나타내는 변수를 명제 변수 (proposition variable)라 부른다. 명제 변수는 일반적으로 소문자 ( \(p,q,r,s \dots\) )를 사용한다.
참/거짓을 진리값이라 하는 데, 일반적으로 참 (Truth)을 \(\text{T}\) , 거짓 (False)을 \(\text{F}\) 로 표기한다.
여러 명제들은 더 작은 명제들로 표현 될 수도 있다. 그러나, 더 작은 명제로 표현될 수 없는 명제도 존재하는 데, 이를 원자 명제 (atomic proposition)라 한다. 이러한 명제들로 부터 새로운 명제들을 파생시킬수 있는데, 이렇게 만들어진 명제를 복합 명제 (compound proposition), 기존 명제에 작용해 새로운 복합 명제를 만들어내는 것을 논리 연산자 (logic operator)라 한다.
논리 연산자는 기존 명제에 새로운 의미를 연결한다고 해서 논리적 연결사(logical connective)라 표현을 쓰기도 한다. 이러한 명제들을 다루는 논리를 명제 논리 (Propositional logic)이라 부른다.
논리 연산자를 소개하기에 앞서서 진리표 (Truth table)를 소개하고 가자. 진리표는 어느 명제가 가질수 있는 진리 값을 모두 나열한 것으로 첫 행에는 표기할 명제들을, 아래 행에는 각 열의 첫번째 명제가 가질 수 있는 진리 값을 기술한다. 독립적인 명제들을 왼쪽에 오른쪽에 해당 명제들로 만들어진 복합 명제를 기술한다.
예를 들어서 두 개의 명제 \(p, q\) 와 이 둘로 이루어진 복합 명제 \(r\) 이 있다면, 다음과 같이 쓸 수 있다.
\(p\) |
\(q\) |
\(r\) |
T |
T |
|
T |
F |
|
F |
T |
|
F |
F |
\(r\) 이 있는 열의 각 행에는 \(p,q\) 의 진리값에 따른 \(r\) 의 진리값이 들어간다. 어느 한 복합 명제 \(r\) 이 \(p_1, p_2, p_3, \dots p_n\) 의 독립 명제들로 이루어져 있다면, 진리표는 총 \(2^n+1\) 개의 행을 가지게 된다 2 . 따라서 진리표는 적은 독립 명제들을 가진 복합 명제의 판정에는 사용가능하지만, 많은 명제들을 가지고 있는 복합 명제의 판정에는 비효율적이다.
논리 연산자(Logic operator)
기초적인 논리 연산자에 부정 (negation), 연언 (conjunction) 그리고 선언 (disjunction)이 있다.
명제 \(p\) 에 대해, ” \(p\) 의 부정”은 \(\neg p\) 로 표기하며, ” \(p\) 가 아닌 경우”를 의미한다.
\(p\) |
\(\neg p\) |
T |
F |
F |
T |
부정 기호는 매우 다양하다. 정의에 쓰인 \(\neg p\) 뿐만 아니라, \(\sim p, !p, p', Np, -p, \overline{p}\) 들도 쓰인다. 단순히 \(\text{not } p\) 로 표기하기도 한다. \(\overline{p}\) 는 집합 기호에서 여집합이나 켤례 복소수의 표기에도 쓰이는 기호라 혼동의 우려가 있어 사용하지 않았다. \(!p\) 는 프로그래밍 언어등에서 부정을 나타내는 데 흔히 쓰인다. 일반적으로 \(NOT\) 연산자라 부른다.
명제 \(p,q\) 에 대해, ” \(p,q\) 의 연언”은 \(p \wedge q\) 로 표기하며, ” \(p\) 가 참이며, \(q\) 도 참이다.”를 의미한다.
\(p\) |
\(q\) |
\(p \wedge q\) |
T |
T |
T |
T |
F |
F |
F |
T |
F |
F |
F |
F |
단순히, \(p \text{ and } q\) 나 \(p \& q\) 로 표기하기도 한다. 일반적으로 \(AND\) 연산자라 부른다.
명제 \(p,q\) 에 대해, ” \(p,q\) 의 선언”은 \(p \vee q\) 로 표기하며, ” \(p\) 가 참이거나 \(q\) 가 참이다.”를 의미한다.
\(p\) |
\(q\) |
\(p \vee q\) |
|---|---|---|
T |
T |
T |
T |
F |
T |
F |
F |
T |
F |
F |
F |
단순히 \(p \text{ or } q\) 로 표기하기도 한다. 일반적으로 “또는” 혹은 “or”로 번역하는 데, 논리학에서의 선언을 의미하는 “또는”과 “or”은 일상 언어에서의 의미와 차이가 있다. 일상 언어에서 해당 단어들은 베타적 (exclusive) 의미를 가지고 있다.
예를 들어 “그 서버는 Windows이거나 Linux이다. “에서 “서버”는 Windows이면서 Linux일 수는 없다. 오직 한가지 경우만이 가능하다. 반면에, 위의 선언(disjunction)은 진리표에서 보이듯이 주어진 두 명제가 모두 참인 경우가 가능하다. 이러한 성질을 포괄적 (inclusive)이라 부른다. 별도의 서술이 없을 경우 논리학에서 선언은 모두 포괄적으로 다루어진다. 베타적 의미의 선언은 따로 정의되어 있다. 일반적으로 \(OR\) 연산자라 부른다.
명제 \(p,q\) 에 대해, ” \(p,q\) 의 베타적 선언”은 \(p \oplus q\) 로 표기하며, ” \(p\) 나 \(q\) 둘 중 하나만이 참이다.”를 의미한다.
\(p\) |
\(q\) |
\(p \oplus q\) |
|---|---|---|
T |
T |
F |
T |
F |
T |
F |
F |
T |
F |
F |
F |
\(p \veebar q, p + q, p \text{ xor } q\) 로 쓰기도 한다. 별도의 베타적 선언 기호를 쓰지않고 포괄적 선언으로 표기할 수도 있다. 진리표를 기준으로 \(p \oplus q\) 는 \((p \vee q) \wedge \neg(p \wedge q)\) 와 같다. 일반적으로 \(XOR\) 연산자라 부른다.
조건문(Conditional Statement)
위의 기본 연산자들 외에 조건문 이라는 방법으로 명제들을 결합할 수도 있다.
명제 \(p,q\) 에 대해, 조건문 ” \(p \rightarrow q\) “는 “만약, \(p\) 이면, \(q\) 이다.”를 의미한다. \(p \rightarrow q\) 는 \(p\) 가 참인데, \(q\) 가 거짓일 경우에 거짓이고, 나머지 경우에는 모두 참이다. \(p \rightarrow q\) 에서 \(p\) 는 전제(premise)라 하며, \(q\) 는 결론(conclusion)이라 한다.
\(p\) |
\(q\) |
\(p \rightarrow q\) |
|---|---|---|
T |
T |
T |
T |
F |
F |
F |
F |
T |
F |
F |
T |
\(p \rightarrow q\) 가 조건문이라 불리는 이유는 \(q\) 의 진리값이 \(p\) 의 진리값에 의존하기 때문이다. 이 조건문을 나타내는 표현도 매우 다양한데 다음이 있다.
\(p \rightarrow q\) |
||
if \(p\), then \(q\) |
if \(p\) , \(q\) |
\(p\) implies \(q\) |
\(p\) is sufficient for \(q\) |
a necessary condtion for \(p\) is \(q\) |
\(q\) when \(p\) |
\(q\) if \(p\) |
\(q\) whenever \(p\) |
\(q\) unless \(\neg p\) |
a sufficient condition for \(q\) is \(p\) |
\(q\) follows from \(p\) |
\(p\) only if \(q\) |
\(p\) only if \(q\) |
\(q\) is necessary for \(p\) |
\(q\) provided that \(p\) |
” \(p\) only if \(q\) “란 표현이 조금 혼동이 올 수도 있는데, ” \(p \rightarrow q\) “가 참임을 기본 전제로 두자, 이때, \(q\) 가 참이 아니면, \(p\) 도 절대로 참일 수 없다. \(p\) 가 참이기 위해서는 \(q\) 가 반드시 참이여만 한다. 때때로 ” \(p\) only if \(q\) “를 \(q \rightarrow p\) 로 받아들이는 경우도 있는 데, 완전히 반대로 해석한것이다. 자주 발생하는 실수이니 주의해야 한다. 많은 경우 수학적 정리와 문제들은 명제 기호로 쓰여있지 않다. 때문에 이를 해석할 때, 주어진 규칙에 맞게 해석했는지 유의해야 한다.
조건문과 같은 진리표를 가지는 복합 명제도 있는데, \(p \rightarrow q\) 는 \(\neg (p \wedge \neg q)\) 와 같은 진리 값을 가진다.
\(p\) |
\(q\) |
\(p \rightarrow q\) |
\(\neg (p \wedge \neg q)\) |
|---|---|---|---|
T |
T |
T |
T |
T |
F |
F |
F |
F |
F |
T |
T |
F |
F |
T |
T |
주어진 조건문 \(p \rightarrow q\) 에 기반해, 명제의 순서를 바꾸거나 부정들을 이용해 새로운 명제들을 만들 수 있다. 이들을 각각 역 (converse), 대우 (contrapositive), 그리고 이 (inverse)라 부른다.
명제(propostion) |
역(converse) |
대우(contrapositive) |
이(inverse) |
|---|---|---|---|
\(p \rightarrow q\) |
\(q \rightarrow p\) |
\(\neg q \rightarrow \neg p\) |
\(\neg p \rightarrow \neg q\) |
이 중 대우는 본래 명제와 같은 진리값을 가진다. 대우가 참이면 본 명제도 참이고, 대우가 거짓이면 본 명제도 거짓이다. 역이나 이는 이런 성질을 가지지 않는다. 일반적으로 역이나 이의 진리값이 정해진다고 해도, 이를 통해 본래 명제의 진리값을 판정할 수는 없다.
다음의 진리 표를 참고하자.
\(p\) |
\(q\) |
\(p \rightarrow q\) |
\(\neg q \rightarrow \neg p\) |
\(q \rightarrow p\) |
\(\neg p \rightarrow \neg q\) |
|---|---|---|---|---|---|
T |
T |
T |
T |
T |
T |
T |
F |
F |
F |
T |
T |
F |
T |
T |
T |
F |
F |
F |
F |
T |
T |
T |
T |
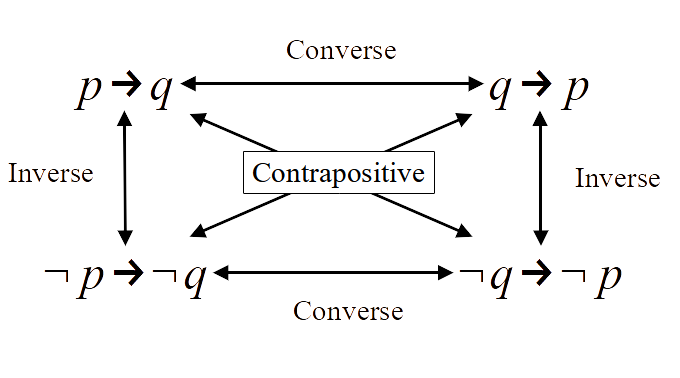
명제, 역, 대우의 구조 다이어그램
다이어그램에서 보이다 시피, 대우는 조건문에 역과 이를 가한 것과 같다. 이때 순서는 상관없다.
조건문과 조건문의 대우는 서로 동일한 진리값을 공유하는 데, 이는 조건문을 이루는 두 명제 \(p\) 와 \(q\) 의 진리값에 관계없이 가지는 성질이다. 이렇듯 어떤 두 복합 명제가 구성하는 독립 명제들의 진리값과 상관없이 언제나 동일한 진리값을 가질 경우 이 두 명제가 논리적 동치 (Logical equivalence)에 있다 한다. 조건문과 그 대우, 조건문의 역과 조건문의 이는 각각 논리적 동치 관계에 있다.
어느 두 명제가 진리값을 공유함을 나타내는 복합 명제는 쌍조건문 (biconditional statement)이라 한다.
명제 \(p, q\) 에 대해, 쌍조건문 \(p \leftrightarrow q\) 는 \((p \rightarrow q) \wedge (q \rightarrow p)\) 을 의미한다. 쌍조건문은 두 명제 \(p\) 와 \(q\) 가 같은 진리값을 가질 때 참을, 다른 경우에 거짓이다.
\(p\) |
\(q\) |
\(p \rightarrow q\) |
|---|---|---|
T |
T |
T |
T |
F |
F |
F |
F |
T |
F |
F |
T |
이 쌍조건 관계에 있는 두 명제는 한가지 명제의 진리값으로 다른 명제의 진리값을 완전히 결정할 수 있다. 쌍조건문은 두 조건문 \(p \rightarrow q\) 와 \(q \rightarrow p\) 가 모두 참일때 성립한다. 이 둘을 나타내는 표현으로 각각 ” \(p\) only if \(q\) “, ” \(p\) if \(q\) “이 있는데, 일반적으로 이 둘을 같이 써서 ” \(p\) if and only if \(q\) “라 한다. 이외에도 다음의 표현들이 있다.
\(p \leftrightarrow q\) |
|
\(p\) is necessary and sufficient for \(q\) |
if \(p\) then \(q\) and conversely |
\(p\) iff \(q\) |
\(p\) exactly when \(q\) |
논리 연산의 적용 순서(Precedence of Logical Operators)
복합 명제를 작성하게 될 때, 위에 서술한 부정, 선언, 연연 그리고 조건문(쌍조건문)들을 다양하게 조합해서 사용하게 된다. 이때, 해당 연산자들의 적용 범위와 순서에 대한 규약이 필요하다. 이러한 규정이 없는 경우 한 복합 명제가 적용 순서와 범위에 따라 다른 명제가 될 수 있기 때문이다.
예로 다음을 보자.
\[p \vee q \wedge \neg r\]
괄호(parentheses)로 연산 순서를 정해 묶어 보면, \((p \vee q) \wedge \neg r\) 이나 \(p \vee (q \wedge \neg r)\) 가 가능하다. 위의 복합 명제는 이 두 명제중 어느 명제를 의미하는가? 연산의 순서가 정해지지 않을 경우 이러한 구분이 불가능하다. 부정, 선언, 연언, 조건 그리고 쌍조건 5가지의 연산자는 다음과 같은 우선순위를 가진다.
Operator |
Order |
|---|---|
\(\neg\) |
1 |
\(\wedge\) |
2 |
\(\vee\) |
3 |
\(\rightarrow\) |
4 |
\(\leftrightarrow\) |
5 |
따라서 예시로 나온 \(p \vee q \wedge \neg r\) 는 \(p \vee (q \wedge \neg r)\) 을 의미한다. 적용 순서에 더해, \(\neg\) 는 뒷 복합 명제 전체나 복합명제를 이루는 단일 명제에 적용 될 수도 있다. 괄호로 구분 되어있지 않을 경우 \(\neg\) 는 가장 짧은 명제에 적용된다.
즉, \(\neg r \wedge p \rightarrow q\) 는 \((\neg r) \wedge p \rightarrow q\) 를 의미한다. 전체 복합명제의 부정을 취하고 싶다면, 괄호를 사용해 \(\neg(r \wedge p \rightarrow q)\) 로 표기해야 한다.
복합 명제의 성질 (Properties of Compound Proposition)
복합 명제는 명제들의 결합 구조에 따라 여러가지 성질을 가지게 된다. 특히 진리값에 대해, 합성된 복합 명제는 이루는 명제들의 진리값에 보편적으로 의존하지만, 특정 명제들은 구성 명제들의 진리값에 관계 없이 일관된 진리값을 유지할 수도 있다. 이러한 성질을 가지는 복합 명제를 항진 명제 와 모순 명제 라 부른다. 영어로 각각 tautology , contradiction 이라 한다.
복합 명제 중 항진, 모순도 아닌 명제를 contingency 하다라 한다.
논리적 동치 (Logical equivalence)
복합 명제 \(p\) 와 \(q\) 에 대해, 명제 \(p \leftrightarrow q\) 가 항진 명제(tautology)일 때, 이 두 명제가 논리적 동치 (Logical equivalence) 관계에 있다라 하고, 이를 \(p \equiv q\) 로 표기한다.
\(\equiv\) 외에 \(\Leftrightarrow\) 표기도 사용한다. 유의점은 논리적 동치는 논리적 연결사, 연산자가 아니다. 이는 단지 명제들 사이의 논리적 관계를 나타낼 뿐이고 단순히, ” \(p \rightarrow q\) 는 항진 명제이다”를 의미한다. 동치 관계에 있는 명제의 파악과 구성은 여러 명제의 진리값을 판별하는 데 매우 중요하다. 특정 명제의 진리값 판별이 매우 어려운 경우라도, 이와 동치 관계인 명제는 손쉽게 판정이 가능할 수도 있기 때문이다.
빈번히 쓰이는 논리적 동치 관계중 하나로 드모르간의 법칙(De Morgan’s law)이 있다.
\[\begin{split}\neg (p \wedge q) \equiv \neg p \vee \neg q\\ \neg (p \vee q) \equiv \neg p \wedge \neg q\end{split}\]
이 법칙은 확장해 \(n\) 개의 명제 \(\{p_i \}_{i=1}^n\) 에 대해 다음과 같이 쓸 수 있다.
\[\begin{split}\neg(p_1 \vee p_2 \vee \dots p_n) \equiv (\neg p_1 \wedge \neg p_2 \wedge \dots \wedge \neg p_n)\\ \neg(p_1 \wedge p_2 \wedge \dots \wedge p_n) \equiv (\neg p_1 \vee \neg p_2 \vee \dots \vee \neg p_n)\end{split}\]
줄여쓰면, \(\neg(\bigvee_{i=1}^n p_i) \equiv \bigwedge_{i=1}^n (\neg p_i)\) , \(\neg(\bigwedge_{i=1}^n p_i) \equiv \bigvee_{i=1}^n \neg p_i\) 로 쓸 수 있다. 이 확장된 드모르간의 법칙의 증명은 수학적 귀납법을 사용해야 한다. 귀납법의 증명 이후 단원에서 자세한 내용을 보도록 하자.
혼동하지 말아야하는 점이 이후 대수 관계에서 나오는 동치 관계(equivalent relation)와 동치류(equivalence class)이다. 여기서 서술하는 논리적 동치와 동치 관계는 적용 대상이 다르다. 논리적 동치 관계는 명제들끼리 이루는 논리적 관계를, 동치 관계는 집합속 원소들 사이에 정의된 관계의 성질을 의미한다. 이 동치 관계는 논리학에서 동일성 관계라 부른다. 이 관계도 논리적 동치 관계에 속한다.
자세한 사항은 집합과 대수 공간을 볼 때 다루도록 하자.
충족성(statifiablility)
복합 명제에 대해, 복합 명제가 참인 진리값을 가지게 만드는 개별 명제들의 진리값 조합이 존재한다면, 이를 충족하다 (satisfiable)라 한다. 이러한 진리값 조합이 존재하지 않는다면, 이를 불충족하다 (unsatisfiable)라 한다. 충족성을 가지는 명제는 모순명제가 아니다. 즉, 항진 명제(tautology)나 contingency인 명제이다. 불충족한 명제는 해당 명제의 부정이 항진 명제인 것과 논리적 동치 관계를 이룬다.
어느 복합 명제가 충족성을 만족하느냐 만족하지 않느냐를 판정하는 문제는 복합 명제를 이루는 구성 명제의 수가 많을 수록 어려워진다. 적은 숫자의 경우는 단순히 진리표를 사용해서 보일 수 있지만, \(n\) 개의 명제로 이루어진 복합 명제는 \(2^n\) 의 경우의 수가 존재하게 된다. 이를 판정할 수 있는 효율적인 기계적 절차는 존재하지 않는다. 다만, 특정 범주의 명제들에 대해 실용적으로 판정 가능한 방법들이 연구되었다.
술어 (Predicate)
명제만으로 수학의 모든 문장을 표현할 수 있다면 좋겠지만, 실제로는 불가능하다. 대표적으로 다음과 같은 문장들을 생각해보자.
자연수 \(x\) 가 \(x=2\) 이다.
유리수 집합에 \(x^2 =3\) 을 만족하는 어떤 유리수 \(x\) 가 존재한다.
모든 실수 \(x\) 에 대해, 정수 \(n\) 이 존재해, \(n < x < n+1\) 을 만족한다.
윗 문장들의 진리값에 대해 생각해보자 이들은 \(x\) 가 실제로 어느 대상이냐에 따라 문장의 진리값이 달라진다. “자연수 \(x\) 가 \(x=2\) 이다.”는 \(x\) 가 \(2\) 일 경우 참이지만, \(x\) 가 \(2\) 가 아닌 다른 자연수일 경우 거짓이 된다. 윗 문장들은 어느 특정한 대상이 아니라 특정한 범주에 대한 서술이다.
이들은 명제 논리의 언어로 표현이 불가능하다. 명제에서는 특정한 범주에 속한 대상을 지칭하는 언어가 없기 때문이다. 명제 논리를 확장한 더 보편적인 논리 체계를 필요로 한다. 이 논리 체계는 명제 논리를 그대로 포함하며 범주와 그 논리적 관계를 서술할 수 있는 체계가 될 것이다.
윗 문장들을 각각 두 부분으로 나누면, 변수: \(x\) 와 문장 속 변수의 성질을 서술하는 부분 문장; 술어 (predicate)로 나눌수 있다. 이 술어는 명제 함수 (propositional function)이라 부른다. 변수 \(x\) 를 받아 진리값을 가지는 명제를 만들어내기 때문이다. 일반적으로 대문자로 \(P, Q, \dots\) 로 표기하며 변수 \(x\) 에 대해, \(P(x)\) 로 쓴다. 여러 변수가 함께 사용될 경우 \(P(x, y, z, \dots)\) 로 쓴다.
어느 명제 \(p\) 는 특정한 값 \(a\) 와 술어 \(P\) 로 표현될 수 있다.
어느 한 술어에 대해, 술어에 필요한 변수의 갯수로 술어를 구분짓기도 한다. 예를 들어서 다음 두 문장을 보자
\(x\) 는 자연수이다.
\(p\) 는 \(q\) 와 동치이다.
이 문장들은 각각 술어 \(P\) = “___ 는 자연수이다” , \(Q\) = “___ 는 ____ 와 동치이다” 와 독립 변수 ( \(x\) ), ( \(p\) , \(q\) )로 이루어져 있다. \(P\) 와 같이 1 개의 독립 변수를 필요로 하는 술어를 일항 술어 \(Q\) 와 같이 2 개의 독립 변수를 필요로 하는 술어를 이항 술어 라 부른다. \(R(x_1, x_2, x_3, \dots , x_n)\) 와 같이 \(n\) 개의 독립 변수 \(\{x_i\}_{i=1}^n\) 를 필요로 하는 술어는 \(n\) 항 술어 이다.
술어는 명제의 구조를 분해해 변수와 그에 대한 서술로 이들을 나눈것이다. 이때, 변수가 가질 수 있는 값의 범주에 따라 술어의 진리값은 달라질 수 있다 1 . 이 때, 여러가지 상황이 가능하다. 어느 술어 \(P(x)\) 에 대해,
\(x\) 범주에서 \(P(x)\) 가 참인 \(x\) 는 존재하지 않는다.
\(x\) 범주에서 \(P(x)\) 가 참인 \(x\) 는 1개 존재한다.
\(x\) 범주에서 \(P(x)\) 가 참인 \(x\) 는 2개 존재한다. \(\vdots\)
- n+1. \(x\) 범주에서 \(P(x)\) 가 참인 \(x\) 는 \(n\) 개 존재한다.
\(\vdots\)
n+2. \(x\) 범주에서 모든 \(x\) 가 \(P(x)\) 가 참임을 만족한다.
\(x\) 범주를 술어 \(P\) 로 정의할 수도 있다. 이 때는 정의에 따라 n+2을 자동으로 만족한다.
양화사(Quantifier)
보편 양화사 (Universal quantifier)
존재 양화사 (Existential quantifier)
양화사의 부정, 결합, 분배 규칙
<!– 논리적 추론과 증명: 196-202 참고 –>
\[\neg (\exists x) Px \rightarrow (\forall x) \neg Px\]\[\neg (\forall x) Px \rightarrow (\exists x) \neg Px\]
추론 규칙 (Rules of Inference)
기본 규칙
조건문 제거
선언 제거
선언 도입
연언 제거
연언 도입
쌍조건 도입
쌍조건 제거
부정 제거
조건 도입
부정 도입
파생 규칙
양화사 규칙
\(\forall\) 제거
\(\forall\) 도입
\(\exists\) 제거
\(\exists\) 도입
이 중 기본 규칙과 파생 규칙은 명제 논리의 추론 규칙이다. 술어 논리는 이에 더해 양화사 규칙을 추가로 포함한다.
보편 양화사의 도입: 임의의 대상 \(u\) 에 대해, A(u) 이다. -> \(\forall x A(x)\)
\(1\) 차와 \(2\) 차 논리 (First and Second order logic)
1차 논리는 원소에만 양화사를 가할 수 있고, 술어에는 한정 기호를 가할 수 없는 술어 논리를 의미한다. 본 문서에서 서술하는 술어 논리는 1차 논리를 의미하며 일반적으로 언급이 없을 경우 대부분의 술어논리는 1차 술어 논리이다. 2차 논리는 변수들의 집합, 술어에도 양화사가 적용가능하다.
이를 소개하는 이유는 특정 대상의 공리를 다지는 상황에서 공리(Axiom)뿐만 아니라 공리꼴(Axiom of schema)을 사용해서 정의하는 경우도 흔하기 때문이다. 공리는 어느 술어와 양화사가 적용되는 대상(원소)로 이루어져있는 1차 술어 논리지만, 공리꼴은 \(2\) 차 논리이므로 술어에도 양화사가 적용될 수 있다. 이를 이용해 임의의 성질을 만족하는 대상들의 존재성을 표현할 수 있다. ZFC 공리계에서 이러한 상황을 살펴볼 수 있다.
증명(Proof)
용어
공리(Axiom)는 참이라고 가정하는 명제를 의미한다. 공리계(Axiom system)는 이러한 공리들을 모아 놓은 것을 의미한다. 공리는 주어진 명제들에 대해, 참 거짓을 판정할 수 있는 전제로써 사용할 수 있다. 이때, 주어진 명제는 참/거짓으로 판정이 되거나 참/거짓 모두 불가능할 수도 있다. 참/거짓으로 판정된 명제는 정리(Theorem)라 불린다.
이러한 명제의 판정을 위한 논증을 증명(Proof)라 부른다. 증명의 과정에서 별개의 명제들을 판별해야 할 수도 있는데, 증명 과정에서 보조로 판정한 명제들을 보조 정리(Lemma)라 부른다. 어떤 명제가 주어진 공리계에서 참이라 판정되었다면, 다른 명제의 증명에서 공리계의 공리와 함께 증명 과정에서 사용가능하다.
별도의 추가적인 공리 없이 바로 증명된 정리에서 유도되는 정리가 있는데, 이는 따름정리(Corollary)라 부른다.
논증
직접증명(Direct proof)
논리적 동치 관계의 연쇄
논리적 동치 관계는 transitivity하다. \(p \leftrightarrow q\) , \(q \leftrightarrow r\) 로 부터 \(p \leftrightarrow r\) 을 유도해낼 수 있다.
\(p \leftrightarrow q\)
\(q \leftrightarrow r\)
\(p \rightarrow q\)
\(p \rightarrow q\)
간접증명(Indirect proof)
대우증명(Proof by contraposition)
모순증명(Proof by contradiction)
다른 증명 방법들
사례별증명(Exhaustive proof/Proof by cases)
진리표를 사용한 증명과 정확히 일치한다. 특정한 경우, 증명해야 하는 복합 명제의 경우가 유한하거나 무한하지만 범주를 나누어 무한한 경우에 대한 증명이 끝나고 유한한 경우만 남을 수도 있다. 이 경우 사례별로 증명을 할 수도 있다.
대표적인 사례가 4색 정리(Four color theorem)의 증명이다. 이 증명은 이러한 사례별 증명에서 사례를 컴퓨터 프로그램으로 증명한 경우이다.
WLOG : Without Loss Of Generality
존재성(Existence) 유일성(Uniqueness)
이곳에 서술한 증명이 모든 증명 전략은 아니다. 상황에 따라서 다양한 증명이 있을 수 있고, 각 수학 분야에서 쓰이는 또다른 증명법이 있기도 하며, 특정 문제에서 특이한 증명이 사용되기도 한다. 그러나 공통적으로 모두 논증의 타당성을 증명하는 과정일 뿐이다. 어느 단 하나의 올바른 증명이 있지는 않다. 증명의 각 단계가 논리적으로 옳다면 모두 올바른 증명이다. 위의 증명 방법들과 논리학에 대한 지식이 있다고 해서 증명을 잘할 수 있지는 않다. 증명에 있어 기계적 방법은 존재하지 않는다. 많은 연습을 통해서 익숙해지는 것밖에 없다.
수학적 귀납법(mathematical induction)은 적어도 고등학교 교육과정에서도 배우지만, 이 단원에서는 생략했다. 정확한 서술을 위해서는 정렬 가능성(order)와 자연수의 성질을 알고있어야하기 때문이다. 귀납법의 가장 큰 약점은 반례의 존재성을 제거할 수 없다는 점이다. 어떤 이론이 단순히 \(1\) 에서 \(1000\) 까지 아니면 계산할 수 있는 큰 수까지에서 참이라 하더라도 이는 특정 범주내에서 참임을 보일 뿐이지, 전체 수에 관해서는 무엇도 보장할 수 없다. 실제로 아주 큰 수에서 대소 관계의 역전이 일어나는 함수들도 존재한다 3 . 수학적 귀납법은 몇가지 공리를 이용해 자연수 범주내에서의 명제 진리값의 일관성을 유지시킬 수 있다.
귀납의 문제와 과학적 방법론
과학적 방법론은 귀납-연역적 방법을 모두 사용하는 방법이다. 한가지 문제는 우리가 자연에 대한 정보를 얻는 방법이 근본적으로 귀납적인 절차라는 점이고 우리가 세운 가설을 검증하는 방법 또한 귀납적인 절차라는 점이다. 때문에 실제 자연과학의 이론은 입증 될 수 없다는 표현을 쓰는 학자들도 많다. 오로지 반증 만이 가능하다. 이러한,
본질적으로, 반증되지 않는다면 참으로 가정한다.
참고문헌
Rosen, K.H., Discrete Mathematics and Its Applications 8th Paperback, ISBN:9781260091991, 2018, McGraw-Hill Education.
이병덕, 논리적 추론과 증명 3rd, ISBN:9788956441290, 2015, 이제이북스.
von Plato, Jan, “The Development of Proof Theory”, The Stanford Encyclopedia of Philosophy (Winter 2018 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/win2018/entries/proof-theory-development/>
Hammack, R.H, Book of Proof 3rd, ISBN:9780989472135, 2019, Richard Hammack
Hepburn, Brian and Hanne Andersen, “Scientific Method”, The Stanford Encyclopedia of Philosophy (Summer 2021 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/sum2021/entries/scientific-method/>.
Judson, T.W, Abstract Algebra: Theory and Applications, ISBN:9781944325107, 2019, Orthogonal Publishing L3C.
각주